| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- 타이타닉데이터
- RCB
- literature review
- 통계대학원
- 케글타이타닉
- 영국석사
- Data Science
- Spatial Data
- 영국통계대학원
- 통계학석사
- factorial design
- statistical experiment
- 코호트연구
- 통계석사
- Machine Learning
- cohort study
- 데이터사이언스
- gam모델
- Smoothing
- 논문제안서
- 영국대학원
- 통계실험
- 통계디자인
- 관찰연구
- mean model
- blocking
- soap film smoothing
- 머신러닝
- Titanic - Machine Learning from Disaster
- 통계예상문제
- Today
- Total
DS and stats
[Statistical design] Factorial designs in blocks(RCB) & GCB 본문
[Statistical design] Factorial designs in blocks(RCB) & GCB
으르미 2022. 3. 15. 08:32
Statistical design - Anova Table
우선 ANOVA란? 구글에 따르면 Analysis of variance, 평균 간의 차이를 분석하는데 사용된 통계적 모델과 그것과 관련된 추정 과정(변동)의 집합 잔차나 오류의 변동, treatment의 변동을 표로 나타낸 것이
eat-drink-study.tistory.com
앞에서 하나의 treatment factor에 대한 RCB에 대해서 정리했었다.
이 blocking은 factorial design과 결합했을 때 더욱 더 효과적이고,
각 block에 있는 실험 유닛의 숫자가 반드시 모든 factors의 레벨의 곱과 같아야 한다.
이것을 RCBF(Randomised complete block factorial)이라고 한다. (treatment factor가 두 개 이상!)

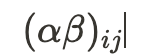
:두 factorial factors \( \alpha \), \( \beta \)사이의 interaction
여기에는 어차피 자유도가 0이 되니까 block factor랑 treatment factor간의 interaction은 없다

여기서 첫번째 mod.blocks 모델의 추정된 분산을 보면 2.6이고
두번째 모델인 mod.no.blocks 모델의 같은 값을 찾아보면, 8.2가 나온다.
즉, 실험이 block화 되지 않았을 때 같은 power를 갖기 위해서는 3.15배의 (8.2/2.6=3.15) 시간이 걸린다는 것이다.
=> 블록화 된 모델이 3.15배 효율이 좋다
Generalised Complete Block Design (GCB)
experiment unit의 블록이 작을수록 균일한 성질을 더 갖게 된다.
즉, 블록이 크면 다른 성질이 포함될 가능성이 크고 블록이 작을 수록 비슷한 성질끼리 모일 가능성이 커진다.
하지만, 블록의 수가 treatment level의 수나 treatment factor의 레벨의 결합가능성의 수? 보다 많아지는 것은 권장되지 않는다.
근데 가끔 큰 블럭의 사이즈인데도 비슷한 성질이 모일 때가 있다.
이 경우, 각 treatment level의 replicates가 속한 디자인을 GCB라고 한다.

이 모델 내에서는 블럭들이랑 treatment factor의 interaction이 가능해짐
근데 문제는 블록 factor가 의미를 가지고 있지 않고 블럭이랑 treatment factor간의 interaction은 유의미한 의미가 존재할 때,
treatment effect는 각 블럭에 따라 해석될 여지가 있다.
그러면 결과를 일반화할 수 없음
ㅜㅜㅜ
그래서 이 경우에는 귀무가설을 \( \tau_i \) =0, for all i 인 treatment effect가 없다고 가정하는
특별한 테스트 통계량?으로 두어야 한다.
또한, F test의 분모로 treatment interaction mean square에 의한 블럭을 사용해야 함!

'Data science - sem 2 > Statistical design of investigation' 카테고리의 다른 글
| Observational study(관찰 연구) 추가 내용/Case-Control Study (0) | 2022.04.19 |
|---|---|
| Observational studies and Causal inference (관찰 연구 및 인과추론) (0) | 2022.04.17 |
| Statistical design - Anova Table (0) | 2022.03.15 |
| Experimental designs with multiple factors (0) | 2022.03.13 |
| statistical design - Mean model vs. Treatment effects model (0) | 2022.03.12 |




